A selection of few projects
Neural Netwoks
We study the distributional properties of linear neural networks with random parameters in the context of large networks, where the number of layers diverges in proportion to the number of neurons per layer. Prior works have shown that in the infinite-width regime, where the number of neurons per layer grows to infinity while the depth remains fixed, neural networks converge to a Gaussian process, known as the Neural Network Gaussian Process. However, this Gaussian limit sacrifices descriptive power, as it lacks the ability to learn dependent features and produce output correlations that reflect observed labels. Motivated by these limitations, we explore the joint proportional limit in which both depth and width diverge but maintain a constant ratio, yielding a non-Gaussian distribution that retains correlations between outputs. Our contribution extends previous works by rigorously characterizing, for linear activation functions, the limiting distribution as a nontrivial mixture of Gaussians
Bassetti,F. Ladelli, L. Rotondo, P. (2024), Proportional infinite-width infinite-depth limit for deep linear neural networks
arXiv:2411.15267
Bassetti,F. Gherardi, M. Ingrosso, A. Pastore, M. Rotondo, P. (2024)
Feature learning in finite-width Bayesian deep linear networks with multiple outputs and convolutional layers.
arXiv:2406.03260
Species sampling models and Bayesian nonparametrics

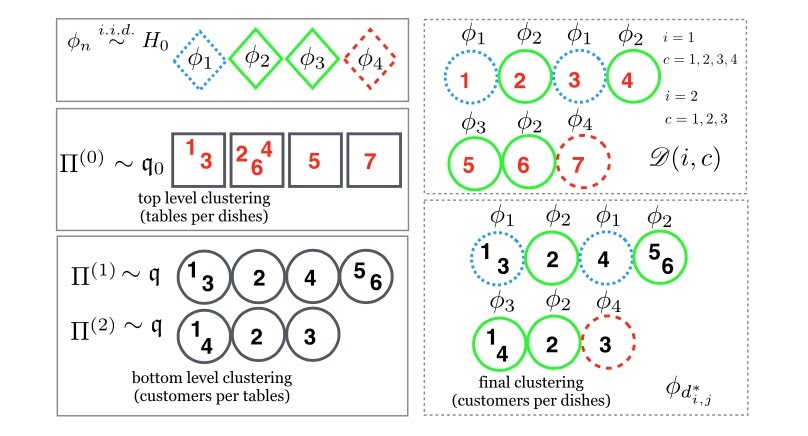
We introduce a general class of hierarchical nonparametric distributions which includes new (e.g. hierarchical Gnedin), and well-known (e.g. Pitman-Yor and NRMI) random measure. Our framework relies on generalized species sampling processes and provides a probabilistic foundation for hierarchical random measures. We show that hierarchical species sampling models have a Chinese Restaurants Franchise representation (see figure) and can be used in Bayesian nonparametric inference.

In a related paper we discuss some asymptotic properties of random partitions induced by species sampling sequences with possibly non-diffuse measure in
Bassetti, F. Ladelli, L. (2020) Asymptotic number of clusters for species sampling sequences with non-diffuse base measure, Statistics & Probability Letters, Elsevier, vol. 162
Kantorovich-Wasserstein distances

We present a method to compute the Kantorovich–Wasserstein distance of order 1 between a pair of two-dimensional discrete distribution (histograms). The main contribution of our work is to approximate the original transportation problem by an uncapacitated min cost flow problem on a reduced flow network of size O(n) [see figure]. When the distance among bins is measured with the 2-norm the reduced graph is parametrized by an integer L. We derive a quantitative estimate on the error between optimal and approximate solution. Given the error, we construct a reduced flow network of size O(n).
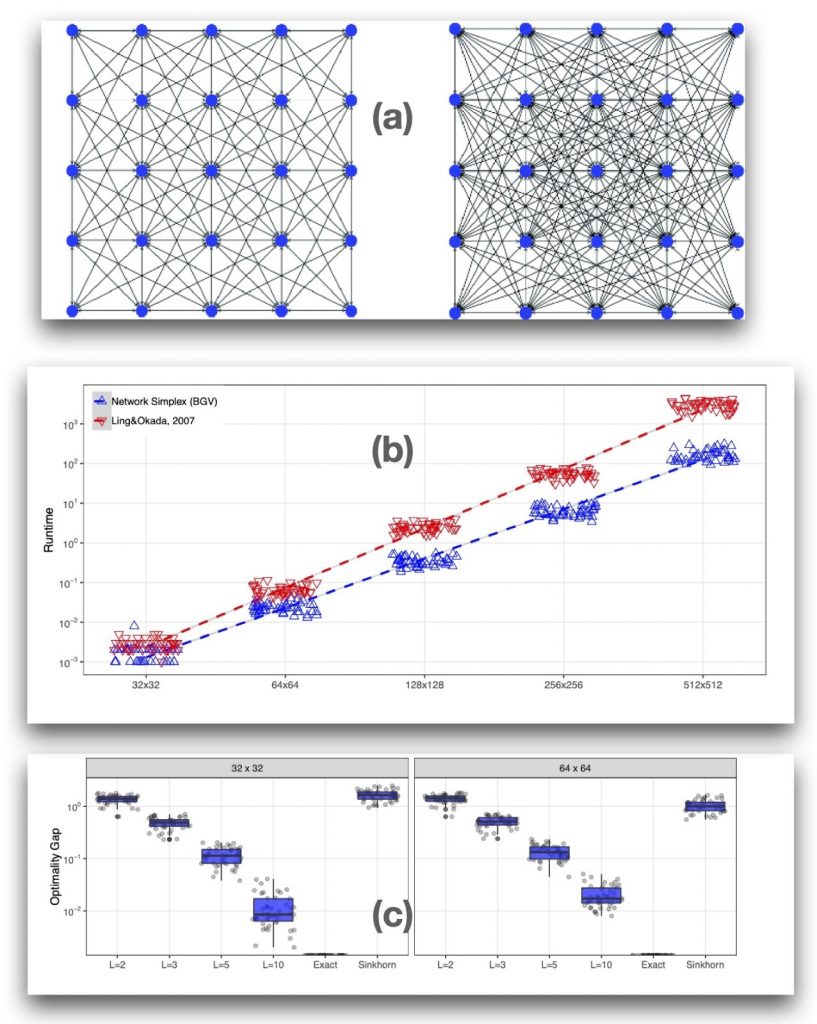
(a) example of reduced network L=2 and L=3; (b) Comparison of runtime between the algorithm proposed in Ling&Okada, 2006 and our for EMD. (c) Comparison of gap between Sinkhorn’s algorithm and our approximation scheme for different L.
F. Bassetti, S. Gualandi, M. Veneroni (2020). On the Computation of KantorovichWasserstein Distances between 2D-Histograms by Uncapacitated Minimum Cost Flows. SIAM Journal on Optimization. 30, No. 3, pp. 2441-2469.
In a related paper we show how these result can be used to compute Wasserstein Barycenters.
Auricchio, G., Bassetti, F., Gualandi, S., Veneroni, M. (2019). Computing Wasserstein Barycenters via Linear Programming. Lecture Notes in Computer Science (Lecture Notes in Artificial Intelligence and Lecture Notes in Bioinformatics) 11494 LNCS, 355- 363.

Bayesian calibration and combination

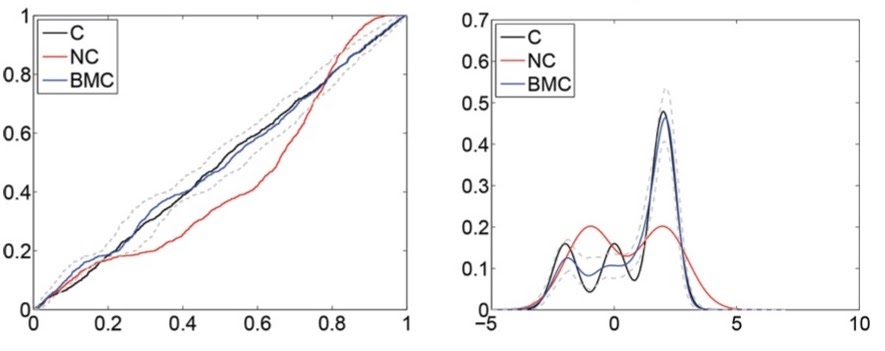
We introduce a Bayesian approach to predictive density calibration and combination that accounts for parameter uncertainty and model set incompleteness through the use of random calibration functionals and random combination weights. We use infinite beta mixtures for the calibration. The proposed Bayesian nonparametric approach takes advantage of the flexibility of Dirichlet process mixtures to achieve any continuous deformation of linearly combined predictive distributions.
